Ondulatória
Escolha o assunto e comece seus estudos!
“A mente que se abre a uma nova ideia jamais volta ao seu tamanho original.”
Albert Einstein
Ondulatória
LISTA 65 – CORDAS
01. (ITA) Uma onda transversal é aplicada sobre um fio preso pelas extremidades, usando-se um vibrador cuja frequência é de 50 Hz. A distância média entre os pontos que praticamente não se movem é de 47 cm. Então, a velocidade das ondas nesse fio é de:
a) 47 m/s
b) 23,5 m/s
c) 0,94 m/s
d) 1,1 m/s
e) 9,4 m/s
02. (FUVEST) Considere uma corda de violão com 50 cm de comprimento, que está afinada para vibrar com uma frequência fundamental de 500 Hz.
a) Qual é a velocidade de propagação da onda nessa corda?
b) Se o comprimento da corda for reduzido à metade, qual a nova frequência do som emitido?
03. (UFPB) A superposição de ondas incidentes e refletidas com mesmas amplitudes dá origem a uma figura de interferência denominada onda estacionária. Nesse sentido, considere uma situação em que uma corda tem uma das suas extremidades fixa a uma parede e a outra extremidade conectada a um oscilador (fonte de vibração) que vibra com uma frequência de 80 Hz. A distância entre o vibrador e a parede é de 8 m. Sabendo que as velocidades de propagação das ondas na corda são de 320 m/s, a onda estacionária na corda está mais bem representada na figura:
04. (FUVEST) A figura a seguir representa imagens instantâneas de duas cordas flexíveis idênticas, C1 e C2, tracionadas por forças diferentes, nas quais se propagam ondas.
Durante uma aula, estudantes afirmaram que as ondas nas cordas C1 e C2 têm:
I. a mesma velocidade de propagação.
II. o mesmo comprimento de onda.
III. a mesma frequência.
Está correto apenas o que se afirma em:
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
Note e adote: A velocidade de uma onda transversal em uma corda é igual a 
, sendo T a tração na corda e μ, a densidade linear da corda.
05. (UNESP) Uma corda elástica, de densidade linear constante μ = 0,125 kg/m, tem uma de suas extremidades presa a um vibrador que oscila com frequência constante. Essa corda passa por uma polia, cujo ponto superior do sulco alinha-se horizontalmente com o vibrador, e, na outra extremidade, suspende uma esfera de massa 1,8 kg, em repouso. A configuração da oscilação da corda é mostrada pela figura 1.
Em seguida, mantendo-se a mesma frequência de oscilação constante no vibrador, a esfera é totalmente imersa em um recipiente contendo água, e a configuração da oscilação na corda se altera, conforme figura 2.
Adotando g = 10 m/s2 e sabendo que a velocidade de propagação de uma onda em uma corda de densidade linear μ, submetida a uma tração T, é dada por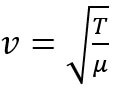 
, calcule:
a) a frequência de oscilação, em Hz, do vibrador.
b) a intensidade do empuxo, em N, exercido pela água sobre a esfera, na situação da figura 2.
06. (FUVEST) Ondas estacionárias podem ser produzidas de diferentes formas, dentre elas esticando-se uma corda homogênea, fixa em dois pontos separados por uma distância L, e pondo-a a vibrar. A extremidade à direita é acoplada a um gerador de frequências, enquanto a outra extremidade está sujeita a uma força tensional produzida ao se pendurar à corda um objeto de massa m0 mantido em repouso. O arranjo experimental é ilustrado na figura. Ajustando a frequência do gerador para f1, obtém-se na corda uma onda estacionária que vibra em seu primeiro harmônico.
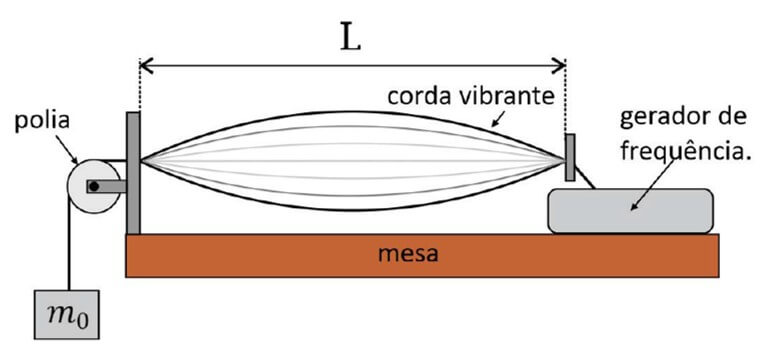
Ao trocarmos o objeto pendurado por outro de massa M, observa-se que a frequência do gerador para que a corda continue a vibrar no primeiro harmônico deve ser ajustada para 2f1. Com isso, é correto concluir que a razão M/m0 deve ser:
a) 1/4
b) 1/2
c) 1
d) 2
e) 4
Note e adote: A velocidade da onda propagando-se em uma corda e diretamente proporcional a raiz quadrada da tensão sob a qual a corda está submetida.
07. (UNESP 2023) Nos instrumentos musicais de corda, as cordas apresentam diferentes espessuras e diferentes densidades lineares de massa, para que aquelas que emitem sons mais graves não precisem ser muito longas, o que inviabilizaria a construção do instrumento.
Para ilustrar o fato de que cordas que emitem sons mais graves precisariam ser muito longas, considere duas cordas, 1 e 2, ambas com extremidades fixas, que apresentem espessuras iguais, mesma densidade linear de massa e que estejam submetidas à mesma força de tração.
Quando essas cordas vibram em seus modos fundamentais, a frequência da onda sonora emitida pela corda 1 é 150 vezes maior do que a frequência da onda sonora emitida pela corda 2. Sabendo que a corda 1 mede L1 = 5 cm, o comprimento L2 da corda 2 deve ser de
(A) 7,5 m.
(B) 8,0 m.
(C) 5,0 m.
(D) 2,5 m.
(E) 1,5 m.
08. (ALBERT EINSTEIN 2023) A velocidade de propagação de uma onda em uma corda pode ser calculada pela expressão 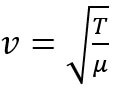, em que T é a intensidade da força com que a corda é tracionada e µ é sua densidade linear de massa. Considere que uma corda tenha massa de 120 g, 3m de comprimento e que se pretenda estabelecer ondas estacionárias nessa corda, como representado na figura.
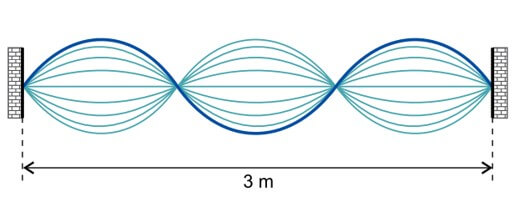
Para que a frequência de oscilação das ondas nessa corda seja de 30 Hz, deve-se submetê-la a uma força de tração de intensidade
(A) 108 N.
(B) 144 N.
(C) 216 N.
(D) 180 N.
(E) 72 N.
09. (PUC) Um homem mantém em equilíbrio estático um bloco preso a uma corda de densidade linear igual a 0,01 kg/m, conforme a figura.
Determine a massa m do bloco, sabendo que as frequências de duas harmônicas consecutivas de uma onda estacionária no trecho vertical de 2 m da corda correspondem a 150 Hz e 175 Hz.
a) 102 g
b) 103 g
c) 104 g
d) 105 g
e) 106 g
10. (PUC) Uma corda de 1,0 m de comprimento está fixa em suas extremidades e vibra na configuração estacionária, conforme a figura a seguir.
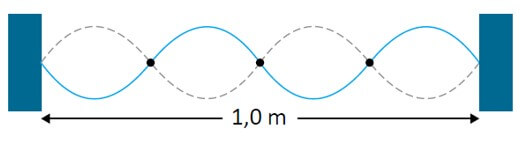
Conhecida a frequência de vibração igual a 1000 Hz, podemos afirmar que a velocidade da onda na corda é:
a) 500 m/s
b) 1000 m/s
c) 250 m/s
d) 100 m/s
e) 200 m/s
Respostas
1- A
2-
a) 500 m/s
b) 1000 Hz
3- D
4- B
5-
a) 5 Hz
b) 16 N
6- E
7- A
8- B
9- C
10- A
