Mecânica
Escolha o assunto e comece seus estudos!
“Se eu vi mais longe, foi por estar sobre ombros de gigantes.”
Isaac Newton
Dinâmica
LISTA 29 – ENERGIA MECÂNICA – SISTEMAS CONSERVATIVOS
01. (ENEM) Uma das modalidades presentes nas olimpíadas é o salto com vara. As etapas de um dos saltos de um atleta estão representadas na figura:
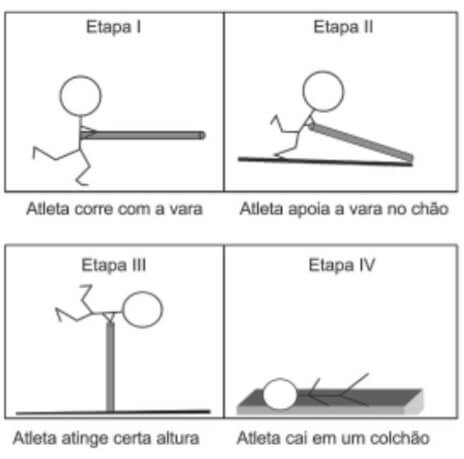
Desprezando-se as forças dissipativas (resistência do ar e atrito), para que o salto atinja a maior altura possível, ou seja, o máximo de energia seja conservada, é necessário que
a) a energia cinética, representada na etapa I, seja totalmente convertida em energia potencial elástica representada na etapa IV.
b) a energia cinética, representada na etapa II, seja totalmente convertida em energia potencial gravitacional, representada na etapa IV.
c) a energia cinética, representada na etapa I, seja totalmente convertida em energia potencial gravitacional, representada na etapa III.
d) a energia potencial gravitacional, representada na etapa II, seja totalmente convertida em energia potencial elástica, representada na etapa IV.
e) a energia potencial gravitacional, representada na etapa I, seja totalmente convertida em energia potencial elástica, representada na etapa III.
02. (FUVEST) Helena, cuja massa é 50 kg, pratica o esporte radical bungee jumping. Em um treino, ela se solta da beirada de um viaduto, com velocidade inicial nula, presa a uma faixa elástica de comprimento natural L0 = 15 m e constante elástica k = 250 N/m. Quando a faixa está esticada 10 m além de seu comprimento natural, o módulo da velocidade de Helena é
a) 0 m/s
b) 5 m/s
c) 10 m/s
d) 15 m/s
e) 20 m/s
Note e adote: Aceleração da gravidade: 10 m/s2.
A faixa é perfeitamente elástica; sua massa e efeitos dissipativos devem ser ignorados.
03. (FUVEST) Um esqueitista treina em uma pista cujo perfil está representado na figura abaixo. O trecho horizontal AB está a uma altura h = 2,4 m em relação ao trecho, também horizontal, CD. O esqueitista percorre a pista no sentido de A para D. No trecho AB, ele está com velocidade constante, de módulo v = 4 m/s; em seguida, desce a rampa BC, percorre o trecho CD, o mais baixo da pista, e sobe a outra rampa até atingir uma altura máxima H, em relação a CD. A velocidade do esqueitista no trecho CD e a altura máxima H são, respectivamente, iguais a
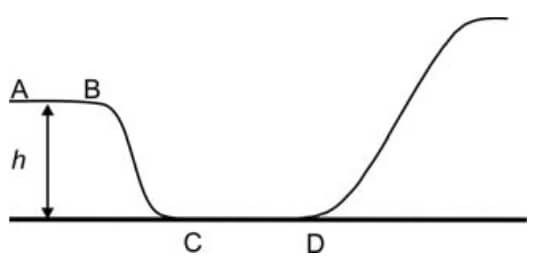
a) 5 m/s e 2,4 m.
b) 7 m/s e 2,4 m.
c) 7 m/s e 3,2 m.
d) 8 m/s e 2,4 m.
e) 8 m/s e 3,2 m.
NOTE E ADOTE
g = 10 m/s2
Desconsiderar:
– Efeitos dissipativos.
– Movimentos do esqueitista em relação ao esqueite.
04. (FUVEST) O projeto para um balanço de corda única de um parque de diversões exige que a corda do brinquedo tenha um comprimento de 2,0 m. O projetista tem que escolher a corda adequada para o balanço, a partir de cinco ofertas disponíveis no mercado, cada uma delas com distintas tensões de ruptura. A tabela apresenta essas opções.
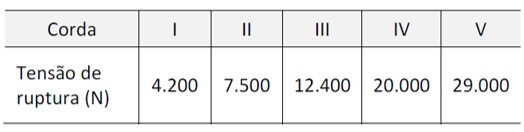
Ele tem também que incluir no projeto uma margem de segurança; esse fator de segurança é tipicamente 7, ou seja, o balanço deverá suportar cargas sete vezes a tensão no ponto mais baixo da trajetória. Admitindo que uma pessoa de 60 kg, ao se balançar, parta do repouso, de uma altura de 1,2 m em relação à posição de equilíbrio do balanço, as cordas que poderiam ser adequadas para o projeto são
(A) I, II, III, IV e V.
(B) II, III, IV e V, apenas.
(C) III, IV e V, apenas.
(D) IV e V, apenas.
(E) V, apenas.
Note e adote: Aceleração da gravidade: 10 m/s2. Desconsidere qualquer tipo de atrito ou resistência ao movimento e ignore a massa do balanço e as dimensões da pessoa. As cordas são inextensíveis.
05. (UNESP) Um caminhão de brinquedo move-se em linha reta sobre uma superfície plana e horizontal com velocidade constante. Ele leva consigo uma pequena esfera de massa m = 600 g presa por um fio ideal vertical de comprimento L = 40 cm a um suporte fixo em sua carroceria.
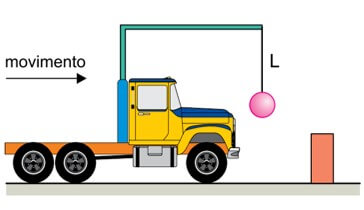
Em um determinado momento, o caminhão colide inelasticamente com um obstáculo fixo no solo, e a esfera passa a oscilar atingindo o ponto mais alto de sua trajetória quando o fio forma um ângulo θ = 60º em relação à vertical.
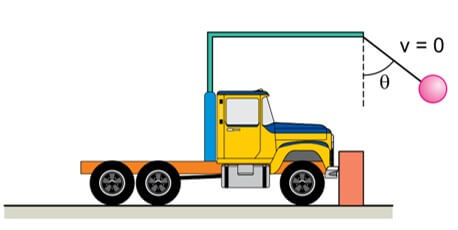
Adotando g = 10 m/s2, cos 60º = sem 30º = 0,5 e desprezando a resistência do ar, calcule:
a) a intensidade da tração no fio, em N, no instante em que a esfera para no ponto mais alto de sua trajetória.
b) a velocidade escalar do caminhão, em m/s, no instante em que ele se choca contra o obstáculo.
06. (FUVEST) Um equipamento de bungee jumping está sendo projetado para ser utilizado em um viaduto de 30 m de altura. O elástico utilizado tem comprimento relaxado de 10 m. Qual deve ser o mínimo valor da constante elástica desse elástico para que ele possa ser utilizado com segurança no salto por uma pessoa cuja massa, somada à do equipamento de proteção a ela conectado, seja de 120 kg?
(A) 30 N/m
(B) 80 N/m
(C) 90 N/m
(D) 160 N/m
(E) 180 N/m
Note e adote:
Despreze a massa do elástico, as forças dissipativas e as dimenões da pessoa; Aceleração da gravidade = 10 m/s².
07. (UNESP) A figura representa o perfil, em um plano vertical, de um trecho de uma montanha-russa em que a posição de um carrinho de dimensões desprezíveis é definida pelas coordenadas x e y, tal que, no intervalo 0 ≤ x ≤ 2p, y = cos (x).
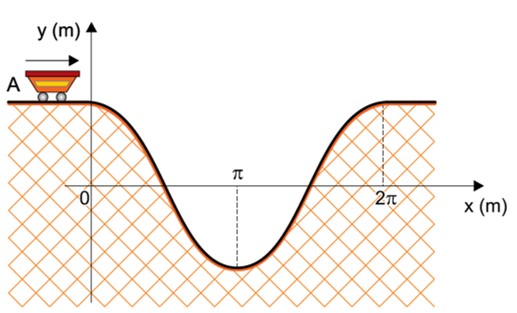
Nessa montanha-russa, um carrinho trafega pelo segmento horizontal A com velocidade constante de 4 m/s. Considerando g = 10 m/s2, ![]() e desprezando o atrito e a resistência do ar, a velocidade desse carrinho quando ele passar pela posição de coordenada
e desprezando o atrito e a resistência do ar, a velocidade desse carrinho quando ele passar pela posição de coordenada ![]() será
será
(A) 10 m/s.
(B) 9 m/s.
(C) 6 m/s.
(D) 8 m/s.
(E) 7 m/s.
08. (UNESP) Uma pequena esfera é abandonada do repouso no ponto 1 e, após deslizar sem rolar pela pista mostrada em corte na figura, perde contato com ela no ponto 2, passando a se mover em trajetória parabólica, até atingir o solo horizontal.
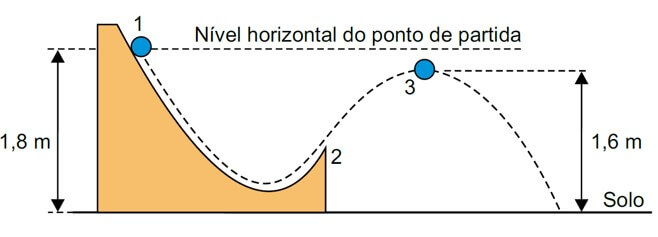
Adotando g = 10 m/s2, desprezando o atrito e a resistência do ar, quando a esfera passar pelo ponto 3, ponto mais alto de sua trajetória fora da pista, a componente horizontal da velocidade vetorial da esfera terá módulo igual a
(A) 1,0 m/s.
(B) 1,8 m/s.
(C) 2,0 m/s.
(D) 1,5 m/s.
(E) 2,5 m/s.
09. (SANTA CASA 2023) A figura representa um pêndulo simples que oscila em um plano vertical entre os pontos X e Z, passando por Y, ponto mais baixo de sua trajetória.
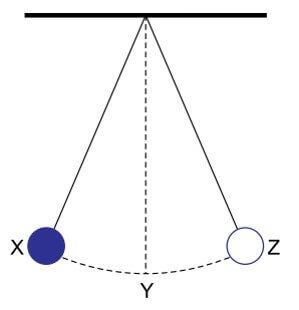
No gráfico, estão representadas as energias potencial gravitacional, cinética e mecânica desse pêndulo, em função de sua posição e em relação ao nível do ponto Y.
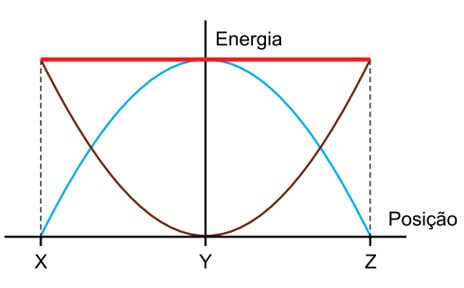
Desprezando as forças dissipativas, as linhas azul, marrom e vermelha indicam, respectivamente, as energias
(A) potencial gravitacional, mecânica e cinética.
(B) mecânica, cinética e potencial gravitacional.
(C) cinética, potencial gravitacional e mecânica.
(D) potencial gravitacional, cinética e mecânica.
(E) cinética, mecânica e potencial gravitacional.
10. (ENEM 2023) Um pai faz um balanço utilizando dois segmentos paralelos e iguais da mesma corda para fixar uma tábua a uma barra horizontal. Por segurança, opta por um tipo de corda cuja tensão de ruptura seja 25% superior à tensão máxima calculada nas seguintes condições:
• O ângulo máximo atingido pelo balanço em relação à vertical é igual a 90°;
• Os filhos utilizarão o balanço até que tenham uma massa de 24 kg.
Além disso, ele aproxima o movimento do balanço para o movimento circular uniforme, considera que a aceleração da gravidade é igual a 10 m/s² e despreza forças dissipativas. Qual é a tensão de ruptura da corda escolhida?
A) 120 N
B) 300 N
C) 360 N
D) 450 N
E) 900 N
Respostas
1- C
2- A
3- E
4- C
5-
a) 3 N
b) 2 m/s
6- E
7- E
8- C
9- C
10- D
